This article introduces a general technique for achieving single-writer non-blocking hash tables at low to negligible cost. The resulting hash table requires no barriers (fences) or locked instructions on architectures such as x86/x86-64. Read operations are lock-free and write operations are fast and bounded. Insertion and deletion are wait-free. Probe sequence mutation is linearized for the common case, bounded and fast. Architectures with relaxed memory models still require barriers.
Non-blocking data structures and their benefits often come at the cost of increased latency because they require additional complexity in the common case. There are plenty of exceptions to this if the requirements of the data structure are relaxed, such as supporting only a bounded level of write or read concurrency.
For this reason, well-designed specialized non-blocking data structures guarantee improved resiliency, throughput and latency in all cases compared to alternatives relying on traditional blocking synchronization primitives such as read-write locks. Specialized concurrent structures are common place in the Linux kernel and other performance critical systems.
Efficient implementations of this mechanism for a cache-friendly double hashed hash table, a robin hood hash set and a hash set have been available in Concurrency Kit under the BSD license for a few years now. Hash tables relying on this transformation have seen more than 3 quadrillion transactions over the internet (and counting) across a diverse workload. This technique is used in a wide array of applications including the Backtrace database.
Motivation
I started working on this problem because of a workload involving bursts of dozens of millions of writes every few minutes and a constant stream of latency bound read requests. For these reasons, I made sure to guarantee system-wide forward progress and forward progress for conflict-free operations in order to improve the flexibility of the data structure. Space efficiency was also important as the target systems were especially memory constrained. The mechanism allows efficient tombstones re-use and probe sequence modification, desirable in long-lived workloads.
The state-of-the-art at the time only provided many-writer many-reader (MWMR) hash table implementations that relied on chaining, CAS2 or complex object re-use constraints. In addition to this, all of these implementations provided MWMR-safety at the cost of increased memory and latency.
Mechanism
By constraining concurrency, a lower overhead lock-free hash table is easily achievable. This section introduces the mechanism with enough details to understand the Concurrency Kit implementations as well as to adapt it to your own data structures. Skip this section if you’re not interested in the details of the actual algorithm itself.
The hash table uses an open-addressed mechanism for collision resolution
and consists of an array of tuples (k, v) where k and v are words that
represent key and value respectively. These tuples are hash table buckets and
are referred to as slots from hereinafter. All slots are initialized to
(E, E). E is a sentinel value that indicates an empty value (no value). T
indicates a tombstone. For demonstration purposes, slots are represented by
the following structure.
struct slot {
/*
* The key field may be the key value or a reference to
* the key value.
*/
void *key;
/*
* The value field may be the value value or a reference to
* the value value.
*/
void *value;
};
The key and value fields must be read and written atomically, preferably
with regular load and store instructions. The hash table needs at least one
version counter. These counters can be striped arbitrarily as long as a slot
maps to exactly one version counter. A version counter is incremented when
the slot it maps to has a probe sequence modified or tombstone re-used.
For illustration purposes in this section, a single version counter called D
is used. The value of D is initially 0. In the code below, an unsigned
integer is used for the version counter. If the unsigned integer is 32-bits, it
is possible for a read operation to observe an inconsistent value if it is
interrupted between 232 (4,294,967,296) write operations. If this is
a realistic concern for your workload, then use a 64-bit counter. For the
purposes of this article, assume that the version counter does not overflow.
The following functions are used in the examples:
ck_pr_load_ptratomically loads a pointer value from the object referred to by the first argument.ck_pr_store_ptratomically stores a pointer into the object referred to by the first argument.ck_pr_store_uintatomically stores an unsigned integer value into the object referred to by the first argument.ck_pr_load_uintatomically loads an unsigned integer from the object referred to by the first argument.ck_pr_fence_loadis a load-load fence.ck_pr_fence_storeis a store-store fence.
These functions are not re-ordered by the compiler. The load and store fences are all unnecessary on TSO architectures such as x86-64. If full fences are mentioned then they are also required on TSO architectures, in absence of modifications. These fences are not needed in pure single writer environments.
Resize
In a single-writer scenario, the resize operation is simple. The old array is copied into a new, resized, array, made visible and then the old array is logically deleted. The old array is destroyed using your preferred safe memory reclamation mechanism. The store operation that makes the new array visible is the linearization point. Linearizability involving writer role migration across processors requires a full fence.
Get
get(struct slot *result, void *key)
{
unsigned int d, d_p;
do {
d = ck_pr_load_uint(&D);
ck_pr_fence_load();
search(result, key);
ck_pr_fence_load();
d_p = ck_pr_load_uint(&D);
} while (d != d_p);
return;
}
The version counter is observed before and after probing the hash table. The reasons for reading the version counter are described later in this article. The search function reads the contents of a slot using the following accesses:
search(struct slot *result, void *key)
{
[...]
result->key = ck_pr_load_ptr(&slot->key);
ck_pr_fence_load();
result->value = ck_pr_load_ptr(&slot->value);
[...]
}
Insert
On insertion, the v value is updated with an atomic store followed by
an atomic store to k. A newly initialized slot transitions from the
(E, E) state to a (k, v) state with an intermediate observable state of
(E, v).
if (ck_pr_load_ptr(&slot->key) == T) {
ck_pr_store_uint(&D, D + 1);
ck_pr_fence_store();
}
ck_pr_store_ptr(&slot->value, value);
ck_pr_fence_store();
ck_pr_store_ptr(&slot->key, key);
Slots that contain tombstones are re-used in order to mitigate tombstone accumulation and help keep probe sequence lengths short. If a tombstone slot is used, then the accompanied version counter update is made visible before completion of the insertion operation.
Delete
ck_pr_store_ptr(&slot->key, T);
ck_pr_fence_store();
The only inconsistent states readers observe in the hash table involve mutations to slots that contain a tombstone. In the following execution history, a reader thread observes a stale key value.
Thread 0 (reader) Thread 1 (writer)
GET(key="apple") slot->key="apple", slot->value="fruit"
k = ck_pr_load_ptr(&slot->key); DELETE(key="apple")
ck_pr_fence_load(); ck_pr_store_ptr(&slot->key, T);
ck_pr_fence_store();
INSERT(key="carrot", value="vegetable")
if (ck_pr_load_ptr(&slot->key) == T) {
ck_pr_store_uint(&D, D + 1);
ck_pr_fence_store();
}
ck_pr_store_ptr(&slot->value, value);
ck_pr_fence_store();
ck_pr_store_ptr(&slot->key, key);
v = ck_pr_load_ptr(&slot->value);
The reader has observed the inconsistent (k = "apple", v = "vegetable"). In order to address
this, the version counter is read before and after the slot read operations in get.
Thread 0 (reader) Thread 1 (writer)
GET(key="apple") slot->key="apple", slot->value="fruit"
d=ck_pr_load_uint(&D);
ck_pr_fence_load();
k=ck_pr_load_ptr(&slot->key); DELETE(key="apple")
ck_pr_fence_load(); ck_pr_store_ptr(&slot->key, T);
ck_pr_fence_store();
INSERT(key="carrot", value="vegetable")
if (ck_pr_load_ptr(&slot->key) == T) {
ck_pr_store_uint(&D, D + 1);
ck_pr_fence_store();
}
ck_pr_store_ptr(&slot->value, value);
ck_pr_fence_store();
ck_pr_store_ptr(&slot->key, key);
v= ck_pr_load_ptr(&slot->value);
ck_pr_fence_load();
d_p = ck_pr_load_uint(&D);
if (d != d_p)
retry;
Inconsistent slot states are only observable by concurrent get operations
that observe slots before deletion and after re-use. If slot re-use is observed
then the accompanied version counter update was ordered prior to it (line 10).
If D + 1 is observed, then the slot key must be T or updated key value
(which implies an up to date and consistent value field due to the fence
on line 14). If the old slot key and new value were observed, then the old value of
D must have been observed.
Probe Sequence Modification
Some open-addressed hash tables require modification of an item’s probe sequence. The versioning scheme described here allows for this, and is utilized by Concurrency Kit hash tables to opportunistically reduce probe sequence lengths.
/* Original points to the original location of the slot. */
struct slot *original;
/* New points to the new location of the slot. */
struct slot *new;
/*
* Insert a copy of the slot in a new location. The insertion
* state machine is re-used.
*/
ck_pr_store_ptr(&new->value, original->value);
ck_pr_fence_store();
ck_pr_store_ptr(&new->key, original->key);
/*
* If the version counter update is visible, then
* so must the updated key-value slot.
*/
ck_pr_fence_store();
ck_pr_store_uint(&D, D + 1);
ck_pr_fence_store();
/*
* If the original slot is re-used, or observed as deleted,
* then the update to the version counter would be visible.
*/
ck_pr_store_ptr(&original->key, T);
ck_pr_fence_store();
As noted in the following section, this is operation isn’t wait-free without some modifications. For example, linearizability is violated if the writer terminates at line 19. Linearizability is achievable with a few modifications (essence of which is outlined in the following section).
Correctness
State-based reasoning is used to provide an informal but clear proof of correctness. The states are represented as 3-tuples that are constituted by the key, value and a version counter. The 3-tuple is always accessed in the following manner by a reader:
ck_pr_load_uint(&c); /* Read version counter. */
ck_pr_fence_load();
ck_pr_load_ptr(&a); /* Read key field. */
ck_pr_fence_load();
ck_pr_load_ptr(&b); /* Read value field. */
ck_pr_fence_load();
ck_pr_load_uint(&c); /* Read version counter again. */
The order of observation is defined as (c, a, b). A reader may
observe any combination of values moving forward in the state
machine. A read operation conflicts with a write operation if the
value of the version load in line 1 does not match the value of the version
load in line 7.
Insertion
The state machine below illustrates the lifecycle of a slot as it transitions from empty (state 1), to occupied (state 3), to deleted (state 5) and then finally to occupied again (state 7).
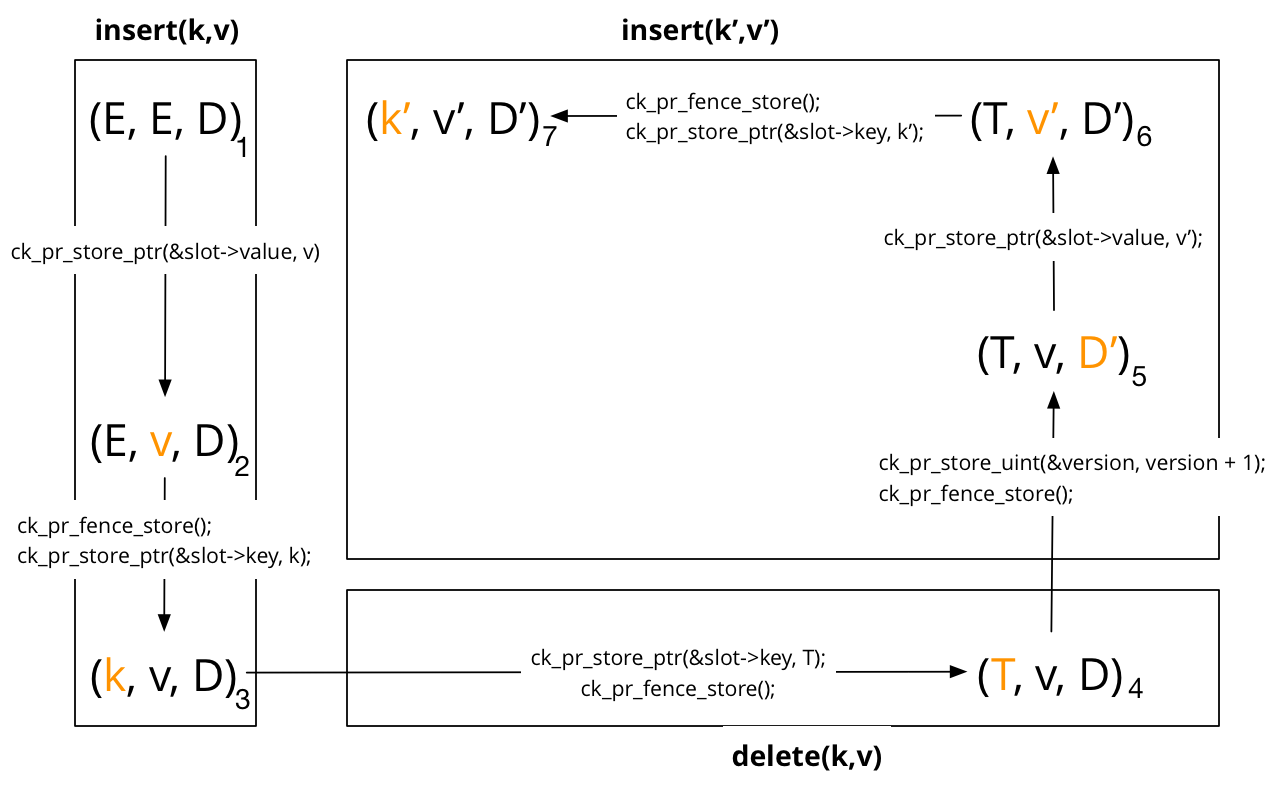
It is possible for a reader to observe an inconsistent slot
but this is a conflicting operation requiring a reader to retry the
get operation. In the state machine diagram above, consider (k, v') to be an
inconsistent state in that (k,v') was never inserted into the hash table.
If the reader was to observe the value k then the preceding load operation on
the version counter occurred on state 3 or 4. This means the reader has
observed the version D. In order for the reader to observe value v'
then it must be that the version is D'. This is because v' is only
set after the version is set to D' in state 5.
If the writer was to crash at any point during these operations, there are no inconsistent slots and readers are only required to restart the load operation once. Readers are linearized by the last load of a key field once the version number check has passed. If the role of active writer can be transferred across threads, then the version counter must be incremented during insertion before any slot field is over-written. If linearizability is required between writers that execute on different processors then a full fence is also required. This scenario may occur in situations where a writer may crash and then another writer (on another processor) takes over the role of single writer.
Probe Sequence Modification
The requirement for movement is that the key-value pair remains consistent and reachable by readers at all times until a delete operation. In addition to this, re-use of the old slot is permitted at any point. A different representation for the state machine is used here. The key-value pair in the middle slot is being moved into the first slot. A shared version counter is used here that is in the third slot position. The movement is achieved by copying the middle pair into the first slot (completed at state 3), incrementing the version counter (completed after state 4) and then marking the old slot with a tombstone. The ordering of all these operations must be retained.

If a reader observes the tombstone of state 5, then a subsequent load operation on the
version counter observes D'. If the load operation began before the move
operation completed, then D would have been observed. The load operation
retries in this situation since it has observed D and D'. If the old slot is
re-used, a conflicting load operation retries since it observes both D' and D''.
The final state in this machine is covered by the first state machine diagram.
The above implementation is not linearized with respect to writers that can migrate roles (early termination) because the sequential specification of the hash table is violated if termination occurs in states 3 or 4. If termination safety and/or linearizability is a requirement then a full fence is required to order the operations with respect to each other and a writer must always check for the presence of a previously uncompleted operation.
Memory Ordering
This algorithm does not provide strong memory ordering guarantees. If an implementation requires stronger ordering guarantees then synchronizing instructions are required prior to the hash table operations. It is also possible to amortize full barriers with barriers on the update and load path.
Conclusion
There we are, a non-blocking SWMR hash table with no atomic operations or memory barriers on the fast path for TSO that is linearized for the common case. There are still avenues for improvement (barrier deferral being one) and patches are welcome. If you require wait-free reads, then writer non-blocking progress can be sacrificed in favor of grace periods instead of version counter updates.
Acknowledgments
Many thanks to Maged Michael, Mathieu Desnoyers, Olivier Houchard, Paul Khuong, Paul McKenney, Theo Schlossnagle, Wez Furlong and the Backtrace Team for helping make this article more readable. Thanks to NasenSpray for pointing out wait-freedom violation in single-process insertion case without version count deferral.
Follow me at @0xf390 if you found this interesting. Follow Backtrace at @0xCD03.